Inhaltsverzeichnis
Gasballon Fahrtheorie
Aufstieg
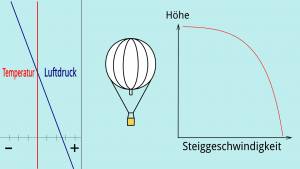
Praller Gasballon
 Auf die Bilder klicken, um sie zu vergrößern.
Auf die Bilder klicken, um sie zu vergrößern.
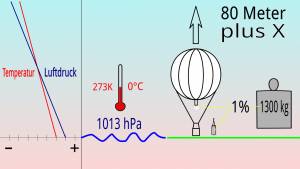
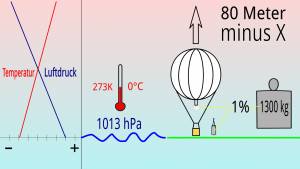
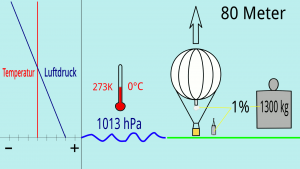
Ein praller Gasballon steigt um 1% in der homogenen Atmosphäre, wenn man seine Masse um 1% veringert. Die homogene Atmosphäre ist 8000 Meter hoch, und ein Prozent entspricht demnach 80 Metern Höhenunterschied. Die Gesamtmasse eines 1000m³ großen Gasballons im Gleichgewichtszustand beträgt bei 1013hPa und 273K/0°C (Normzustand der Gase) 1300kg. Um 80 Meter zu steigen muss die Masse um 13kg verringert werden. Das bedeutet jetzt aber nicht die entsprechende Ballastabgabe, sondern es ist auch zu berücksichtigen, dass das aus dem Füllansatz strömende Gas auch eine Masse hat. Da sich auch der Druck bei einem Höhenunterschied von 80 Metern um 1% reduziert, vergrößert sich das Volumen des Gases um 1 Prozent und es strömt Gas mit einer Masse von einem Prozent der Gasmasse aus dem Füllansatz.
Die homogene Atmosphäre hat auch in allen Höhen die gleiche Temperatur, man spricht hier auch von Isothermie. In der realen Atmosphäre hingegen nimmt die Temperatur meist mit der Höhe ab. Dann steigt der Ballon um 80 Meter plus X. Wobei X umso größer ist, je weniger stabil bzw. je labiler die Atmosphäre geschichtet ist, das heißt je mehr die Temperatur mit der Höhe abnimmt:
Nimmt die Temperatur dagegen mit der Höhe zu, man spricht dann auch von einer Inversion, dann steigt der Ballon um 80 Meter minus X. X ist umso größer, je mehr die Temperatur mit der Höhe zunimmt. Es kann sogar sein, dass der Ballon aufhört zu steigen:
Die Tabelle zeigt am Beispiel eines 1000m³-Gasballons die Relation der Gasmasse zur Ballastmenge um die Veringerung der Gesamtmasse um 1%=13kg zu erreichen.
| Gas | Formel | Dichte kg/m³ | Gerundet kg/m³ | Gasmasse 1% (1000m³) | Ballast-Abgabe |
|---|---|---|---|---|---|
| Vakuum* | 0.0 | 0 | 0 | 13kg | |
| WASSERSTOFF | H2 | 0.08988 | 0.1 | 1kg | 12kg |
| HELIUM | HE | 0.178 | 0.2 | 2kg | 11kg |
| Leuchtgas | H2&CH4&CO | 0.550 | 0.6 | 6kg | 7kg |
| Methan | CH4 | 0.717 | 0.7 | 7kg | 6kg |
| Ammoniak | NH3 | 0.771 | 08 | 8kg | 5kg |
| Luft 100°C* | 0.95 | 0.95 | 9.5kg | 3.5kg |
*Natürlich gibt es kein Gas »Vakuum«, das ideale masselose Traggas gibt es nicht. Von der Dichte her ist das ideale Traggas Wasserstoff, Helium kommt aus Kostengründen nur selten zum Einsatz, Methan und Ammoniak nur in Ausnahmefällen. Und Leuchtgas, auch Stadtgas genannt, war das Gas dass in den Kokereien erzeugt wurde. Zum Vergleich ist Heißluft mit einer Temperatur von 100°C/273K aufgeführt, als »Gas« gibt es Heißluft ebensowenig, sie muss mit einem Brenner erhitzt werden.
Das Modell der homogenen Atmosphäre dient beim Gasballon dazu, die Ballastmenge für den Aufstieg bzw. die benötigte Gasmenge in Abhängigkeit der Höhe des Füllplatzes abzuschätzen. Das Modell der homogenen Atmosphäre entspricht nicht der realen Atmosphäre. Die homogene Atmosphäre kann für Höhenunterschiede bis zweitausend Meter für Berechnungen mit hinreichender Genauigkeit verwendet werden.
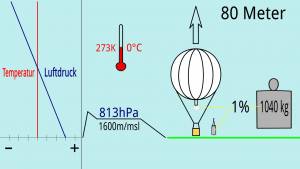
Möchte man beispielsweise mit einem prallen Gasballon von Null auf 1600 Meter Höhe steigen, so sind 1600 Meter zwanzig Prozent von den achtausend Metern Höhe der homogenen Atmosphäre. Zwanzig Prozent der Masse von 1300kg des 1000m³-Gasballons sind 260kg. Die 260kg Masse um die die Gesamtmasse des Gasballons veringert werden muss, setzten sich aus 240kg Ballastsand und 20kg Wasserstoffgas zusammen. Die Rechenmethode funktioniert auch für das Gasvolumen. Wenn zum Füllen des Gasballons auf Meereshöhe 1000m³ benötigt werden, so werden auf 1600m noch 800m³ benötigt. (Achtung beim Bestellen: Gaslieferanten berechnen häufig das Volumen von Gas für einen Druck von 1013hPa und eine Temperatur von 15°C/288K - den Werten der Normatmosphäre für die Meereshöhe).
Das Modell der homogenen Atmosphäre kann auch für Berechnungen verwendet werden, die in größerer Höhe stattfinden. Man muss dann aber beachten, dass die Luftdichte entsprechend geringer ist. Und je nachdem wie stark die Werte von den tatsächlichen Werten abweichen, die Berechnung entsprechend ungenauer wird. Wenn die Genauigkeit reicht, ist bleibt es eine schnelle Methode. Im obiger Grafik wird der Aufstieg ab 1600m/msl dargestellt. Wobei es egal ist, ob es sich um den Start oder um weiteres Steigen handelt. Die Gesamtmasse des Ballons beträgt jetzt nur noch 1040kg, um 80 Meter zu steigen muss die Gesamtmasse nach wie vor um 1% verringert werden - nur beträgt dieses 1% jetzt nur noch 10,4kg.
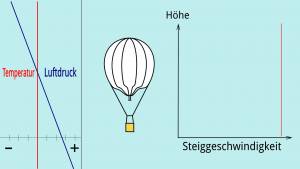
Unpraller Gasballon
Ein unpraller Gasballon, das bedeutet ein Gasballon der nicht vollständig gefüllt ist, steigt mit konstanter Geschwindigkeit bis zu seiner Prallhöhe. Die Prallhöhe ist die Höhe, in der das Traggas die Hülle vollständig ausfüllt. Übersteigt er die Prallhöhe tritt Traggas aus dem Füllansatz aus. Aufgrund der Massenträgheit wird die Gleichgewichtslage etwas überstiegen, was zum richtigen Zeitpunkt durch Ballastabgabe kompensiert werden muss, soll der Ballon nicht wieder ins Sinken kommen.
Steig- und Sinkgeschwindigkeit
Praller Gasballon
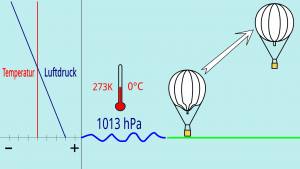
Ein praller Gasballon verliert beim Steigen Auftrieb, da sein Volumen gleich bleibt, die Luftdichte aber mit der Höhe abnimmt und damit das Gewicht der durch ihn verdrängten Luft. Dadurch nimmt auch seine Steigkraft und damit die Steiggeschwindigkeit mit der Höhe ab. Wenn man mit konstanter Geschwindigkeit steigen möchte, muss man stetig Ballast abgeben.
Unpraller Gasballon
Ein unpraller Gasballon steigt oder sinkt mit konstanter Geschwindigkeit, da sein Auftrieb konstant bleibt, denn: Wenn er steigt, dann nimmt zwar die Dichte der verdrängten Luft ab, aber gleichermaßen nimmt das Volumen des Ballons zu. Damit wird die geringere Luftdichte vollständig kompensiert. Wenn er sinkt verhält es sich genau umgekehrt, zwar verdrängt ein immer kleineres Volumen Luft, diese ist jedoch dafür dichter bzw. schwerer. Das ist jeoch nur dann der Fall, wenn die Lufttemperatur in allen Höhen gleich ist, wenn es eine Isothermie gibt.
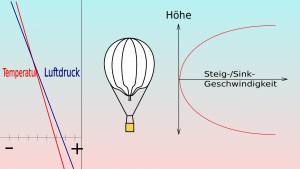
Nimmt die Temperatur mit der Höhe ab, dann gewinnt der Ballon beim Steigen Auftrieb, seine Steiggeschwindigkeit nimmt zu. Umgekehrt verhält es sich beim Sinken, hier verliert er Auftrieb, die Sinkgeschwindigkeit nimmt zu. Dieser Effekt ist umso stärker je labiler die Atmosphäre geschichtet ist. Der Auftriebsverlust wird bei so einer Temperaturschichtung mit jedem Meter den der Ballon sinkt größer. Je länger mit der Ballastabgabe gewartet wird, umso mehr Ballast muss ausgegeben werden.
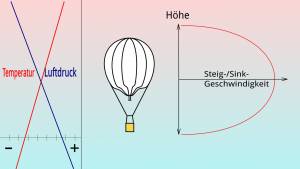
Nimmt die Temperatur mit der Höhe zu - was in einer (Temperatur-)Inversion der Fall ist, dann verliert der Ballon beim Steigen Auftrieb und gewinnt ihn beim Sinken. Daher fährt der Ballon in einer Inversion sehr stabil. Wenn der Ballon in einer Inversion fährt, ist es gut möglich, dass er eine Viertelstunde lang mit einem halben Meter pro Sekunde sinkt, um anschließend wieder eine Viertelstunde mit einem halben Meter zu steigen. Jede Ballastausgabe oder jeder Ventilzug führt hier zur Ballastverschwendung. Die Kunst der Ballonführung liegt darin, zu erkennen, ob der Ballon das Sinken selbständig beenden wird, oder nicht.
Reibungszahl
Doch wieviel Steig- oder Sinkkraft hat jetzt der Ballon, bzw. wieviel Ballast muss ausgegeben werden um eine bestimmte Steigrate zu erreichen? Das Abschätzen zu können dazu dient die Reibungszahl.
Die Reibungszahl berechnet sich aus dem Luftwiderstandsbeiwert (CW-Wert) einer Kugel, dem Querschnitt des Ballons und der Luftdichte von 1,3kg/m³. Sie beträgt für einen Ballon der tatsächlichen Größe von 1000m³ 3,81). Da der Luftwiderstand exponentiell zunimmt, ergibt sich folgende Formel zu Berechnung der Steig-/Sinkkraft:
(Steiggeschwindigkeit m/s) x (Steiggeschwindigkeit m/s) x 3,8 = Steig-/Sinkkraft
Beispiel für Steig-/Sinkgeschwindigkeiten bis 10m/s:
| m/s | ()² | Reibungszahl | S-Kraft kg |
|---|---|---|---|
| 1 | 1 | 3.8 | 3.8 |
| 2 | 4 | 3.8 | 15.2 |
| 3 | 9 | 3.8 | 34.2 |
| 4 | 16 | 3.8 | 60.8 |
| 5 | 25 | 3.8 | 95.0 |
| 6 | 36 | 3.8 | 136.8 |
| 7 | 49 | 3.8 | 186.2 |
| 8 | 64 | 3.8 | 243.2 |
| 9 | 73 | 3.8 | 277.4 |
| 10 | 100 | 3.8 | 380.0 |
Die Reibungszahl ist größer, das heißt es muss mehr Ballast abgeworfen werden, wenn
- der Luftwiderstandsbeiwert (CW-Wert) größer als der einer Kugel ist, beispielsweise bei einem eingedellten2) Ballon.
- zum Luftwiderstand der Hülle auch noch der Luftwiderstand des Korbes und eventuell angehängter Ausrüstungsgegenstände kommt.
- wenn die Luftdichte größer als 1,3kg/m³ ist, beispielsweise wenn der Umgebungsluftdruck größer als 1013hPa oder die Temperatur kleiner als 0°C/273K ist.
Die Reibungszahl ist kleiner, das heißt es muss weniger Ballast abgeworfen werden, wenn
- der Luftwiderstandsbeiwert (CW-Wert) kleiner als der einer Kugel ist, beispielsweise wenn ein unpraller Ballon eine strömungsgünstigere Form annimmt.
- der Luftwiderstand kleiner ist, weil der Querschnitt des unprallen Ballons sich verringert hat.
- die Luftdichte kleiner als 1,3kg/m³ ist, beispielsweise weil der Umgebungsluftdruck kleiner als 1013hPa oder die Temperatur größer als 0°C/273K ist.
Formel Luftdichte:
Dichte = (1,3k/m³) x (QFE)/1013hPA) x 273K / (273 +- T)
*QFE - Umgebungsluftdruck in hPA, *T - Umgebungstemperatur in Kelvin
Die Reibungszahl dient zum Abschätzen der benötigten Ballastmenge, exakt berechnen lässt sich diese nicht, da die dafür notwendigen Daten fehlen. Zum einen lässt sich der Luftwiderstand eines Ballons nicht genau ermitteln, denn es gehört dazu nicht nur die Ballonkugel, sondern auch der Korb und eventuelle Anbauten wie außen hängende Sandsäcke, Kartenbrett, Fahnen, etc. Zum anderen lässt sich der Umgebungsluftdruck (QFE) leicht messen, aber schwieriger gestaltet sich die genaue Ermittlung der Temperatur der umgebenden Luft. Aber grau ist alle Theorie, wenn genug Höhe zum Abfangen vorhanden ist, wird man erst etwas weniger als nach der Berechnung notwendig abwerfen, und dann entsprechend weiter Ballast abgeben. Das ist dann - Gefühlssache.
Abfangen
Gibt man bei einem sinkenden Ballon genaus soviel Ballast ab, dass der Ballon im Gleichgewicht ist, dann sinkt er noch etwa 80 Meter in die Tiefe. Gibt man doppelt soviel Ballast ab wie für die Gleichgewichtslage notwendig, dann sinkt er noch etwa 15 Meter in die Tiefe. Daraus folgt auch, dass wenn man weniger als 80 Meter Höhe zum Abfangen des Ballons zur Verfügung hat, man mehr Ballast abwerfen muss als für die Gleichgewichtslage notwendig ist, und der Ballon dadurch wieder in Steigen kommt - der Ballon überworfen wurde.
Temperatureinfluss
Praller Ballon
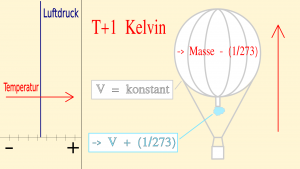
Nimmt die Temperatur eines prallen Gasballons zu - in der Regel durch Sonneneinstrahlung - dann dehnt sich das Füllgas (Traggas) aus, und es strömt Gas aus dem Füllansatz. Dadurch verringert sich die Traggasmasse und dadurch erhöht sich die Tragkraft des Ballons.
Tragkraft = Auftrieb - Traggasmasse
Pro Kelvin Temperaturzunahme verringert sich die Traggasmasse und damit die Gesamtmasse des Ballons um 1/273 und der Ballon steigt entsprechend höher.
Bei der Verwendung von Wasserstoff mit seiner geringen Dichte fällt die Höhenzunahme auch gering aus, der Ballon steigt pro Kelvin Temperaturzunahme um etwa 2,5 Meter. Bei einem dichteren Traggas ist die Höhenzunahme größer. Bei Stadtgas beträgt sie etwa 25 Meter pro Kelvin Temperaturzunahme.
Unpraller Ballon
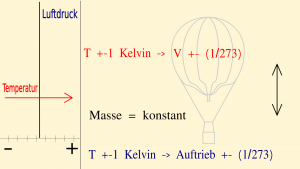
Steigt die Traggastemperatur
Bei einem unprallen Ballon bewirkt die Temperaturzunahme eine Volumenzunahme des Ballons bei gleichbleibender Traggasmasse. Die Volumenzunahme führt zu einem höheren Auftrieb. Und zwar nimmt der Auftrieb um 1/273 zu pro Kelvin Temperaturerhöhung zu. Die Zunahme des Auftriebs ist unabhängig vom verwendeten Traggas, sie hängt ausschließlich von der Gewichtskraft der Umgebungsluft ab. Bei einem Druck von 1013hPa und 0′C/273K beträgt sie bei einem noch vorhandenen Traggasvolumen von 900m³ 4,3kg pro Kelvin Temperaturzunahme und bei einem Traggasvolumen von 600m³ 2,9kg pro Kelvin Temperaturzunahme.
Sinkt die Traggastemperatur
Sinkt die Traggastemperatur - meist durch nächtliche Abstrahlung von Wärmenenergie in den Weltraum oder durch nachlassende Sonneneinstrahlung - dann verringert sich das Volumen des Ballons und er verliert Auftrieb. Die Berechnung ist die Gleiche wie bei der Temperaturzunahme des unprallen Ballons.
Buchtipp
Unsere kleine Einführung in die Fahrtheorie des Gasballons ist hiermit zu Ende. Wer tiefer in die Theorie einsteigen möchte, dem sei das Buch »Gone with the Wind« empfohlen. Das Buch wurde von Astrid Gerhardt und Peter Cuneo überarbeitet und sollte im 4. Quartal 2016 wieder lieferbar sein. Interessenten können sich direkt per E-Mail an Astrid Gerhardt wenden: ag@g-ig.net
Das Buch basiert auf der 1. Auflage, der Inhalt wurde aktualisiert und mit dem einem Kapitel über den Gasballon des Herstellers Padelt, sowie Menschliches Leistungsvermögen ergänzt.
Gliederung:
- Einleitung
- Der netzlose Gasballon und seine Bauteile
- Ausrüstung und Instrumente
- Führung des Gasballons: Theorie und Praxis
- Ballonaufrüst- und Füllhinweise
- Der Padelt Gasballon
- Gefahren und Sicherheit bei der Verwendung von Wasserstoff
- Fahrtvorbereitung für eine Fahrt mit dem Gasballon
- Allgemeine Start-, Fahrt- und Landehinweise
- Verhalten in besonderen Fällen
- Fahrten in den Bergen
- Höhenfahrten und der Gebrauch von Sauerstoff
- Menschliches Leistungsvermögen
- Wettbewerbs- und Rekordfahrten
- Navigation
- Meteorologie
Format ist Din A4 quer als Hardcover, mit ca. 300 Seiten
Sprache: deutsch und englisch